三種の理論課目で出て来る直流回路はだいたいそんなに難しくありません。
高校や大学で電気を専門にしていなくても、
直流回路は知ってるでしょう。中学校でやりますよね。
だから既に$IR=V$の公式は覚えていると思うので、
大して覚える事が無いんです。だから簡単です。
オームの法則だけは覚える
まずは、$IR=V$のオームの法則です。
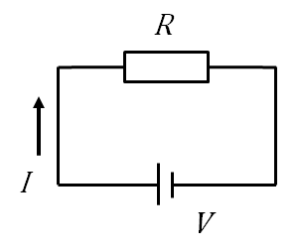
電流×抵抗=電圧。
これはもうずっと使うので忘れることはないでしょう。
ここで、抵抗Rについては、
$R=ρL/S$
(ρ:抵抗率, L:導体長さ, S:導体断面積)
という式もあります。
この式は、$L$か$S$のどっちが上だったか迷いがちです。
これは暗記せずとも、水を流すホースをイメージすれば、
長ければ長い($L$が大きい)ほど水流が少なくなり、→抵抗が大きい
太い($S$が大きい)ほど、水流が多くなること →抵抗が小さい
をイメージすれば理解しやすい、と思います。
合成抵抗の考え方
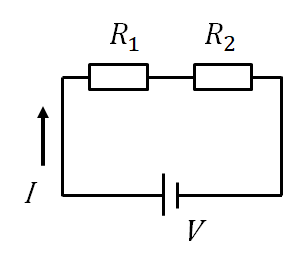
直列の合成抵抗
上の回路の合成抵抗は$R_1+R_2$です。
直列接続の抵抗を合成するには足せば良いだけです。
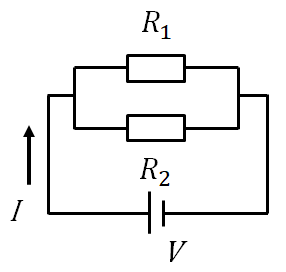
並列の合成抵抗
並列の場合は逆数の和です。
$1/R_1 + 1/R_2$
$ = (R_1 R_2) / (R_1 + R_2) $
和 分の 積 とか呼んで勝手に覚えてる人も居るでしょう。
で、これくらいなら直列は和で、並列は逆数和とパターンで覚えてしまっても良い話ですが、
電験の勉強を進めていくにあたり、覚えることが増えてきます。
だんだんと混乱したりしてくるものです。
これらを公式だからと丸覚えだけせず、少し考えて見れば覚えやすい、
というか覚えるほどのものでも無かったりします。
直列合成抵抗
先ほどの直列回路を考えます。
回路を繋いでいる線には抵抗がないと考えるのが試験問題では普通なので、
$R_1$の右側と、$R_2$の左側は等電位です。
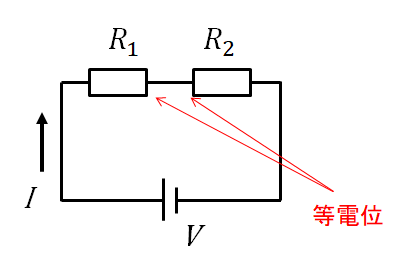
なので、2つの抵抗はつながってるも同然と考えれば良いです。
とはいえ足して計算できるかどうかに疑問があれば、
中学で習った、直流回路の電流はどこでも同じだということを思い出してください。
電流は$R_1$を通った後でも前でも同じ数値です。
$R_1$を通って、$R_2$を通る間に電流に影響はないので、
和で考えても同じです。
$R_1+R_2$
並列合成抵抗
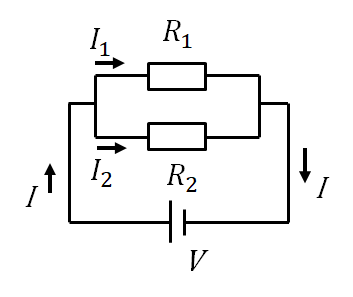
電線間が等電位なら、並列も和じゃダメなのか?
と思うかもしれませんが、並列の場合は電流は二手に分かれますので、
同じようには考えません。
じゃあなぜ並列の合成抵抗は逆数の和なのか?を考えるには、
$I_1$と$I_2$を考えると分かります。
$I_1=V/R_1$
$I_2=V/R_2$
並列の場合は、電圧はどちらに分岐しても同じでしたよね。
ここで、分岐する前の電流$I$は、
$I = I_1 + I_2$ ですから、(これはキルヒホッフの法則です)
$I = V/R_1 + V/R_2$ … [1]
電流$I$は回路全体の電流なので、合成抵抗をRとすると、
$I = V/R$ と表せるので、上の[1]式は
$V/R = V/R_1 + V/R_2$ と書き換えられます。
これはつまり、
$V/R = V(1/R_1 + 1/R_2)$ です。
Vを消せば、
$1/R = 1/R_1 + 1/R_2$
ということで、逆数の和になります。
合成抵抗の式くらいは勝手に覚えるとは思いますが、
成り立ちや意味がわかれば、パターンのように暗記しなくても、
自分で確認したりも出来るという例です。
私は暗記が苦手なので…